Skip to main content

Flash Attention v1 理论篇

Transformer 模型的时候处理速度较慢，且会占用大量的显存。自注意力的时间和内存复杂度是与序列长度的平方成正比。在 GPU 上，计算速度已超过内存速度，并且 Transformers 中的大多数操作都受到内存访问的瓶颈。因此，内存访问模式的优化是加速 Transformer 模型的关键。Flash Attention 是一种高效的自注意力实现，它通过将内存访问模式与计算结合起来，减少了内存带宽的使用，从而提高了性能。

在这个系列中，我们将介绍 Flash Attention 系列的原理和实现。

1. GPU 的层次结构​

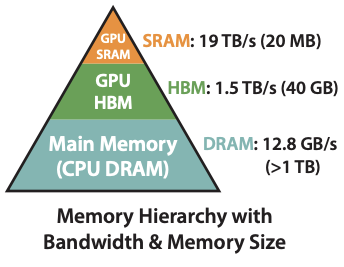
老规矩，我们还是先回顾一下 GPU 的层次结构。GPU 内存层次结构由不同大小和速度的多种形式的内存组成，较小的内存速度较快。例如，A100 GPU 具有 40-80GB 的高带宽内存（HBM），带宽为 1.5-2.0TB/s，并且每个 108 个流处理器有 192KB 的片上 SRAM，其带宽估计约为 19TB/s [44, 45]。片上 SRAM 的速度比 HBM 快一个数量级，但其大小小了多个数量级。

picture 0

2. 标准 Attention​

给定输入序列 Q,K,V∈RN×d\mathbf{Q}, \mathbf{K}, \mathbf{V} \in \mathbb{R}^{N \times d}，其中 NN 是序列长度，而 dd 是头部维度，我们希望计算注意力输出 O∈RN×d\mathbf{O} \in \mathbb{R}^{N \times d}：

S=QK⊤∈RN×N,P=softmax⁡(S)∈RN×N,O=PV∈RN×d,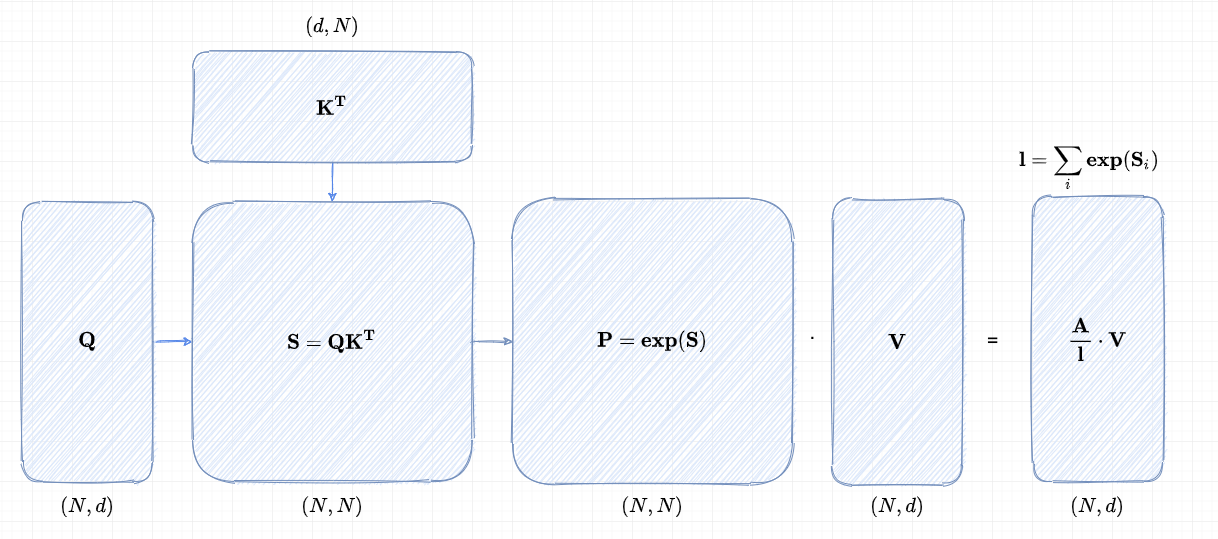\mathbf{S}=\mathbf{Q} K^{\top} \in \mathbb{R}^{N \times N}, \quad \mathbf{P}=\operatorname{softmax}(\mathbf{S}) \in \mathbb{R}^{N \times N}, \quad \mathbf{O}=\mathbf{P V} \in \mathbb{R}^{N \times d},

picture 4

在标准的注意力机制实现中，矩阵 S\mathbf{S} 和 P\mathbf{P} 需要被显式地存储在高速但容量有限的高带宽内存（HBM）中。这种存储方式带来了 O(N2)O(N^2) 的内存开销，这在处理大规模输入时尤其值得关注。

以一个具体实例来看，在 GPT-2 模型中，序列长度 NN 为 1024，而每个特征的维度 dd 仅为 64，即 N≫dN \gg d。由于注意力机制的核心操作（如 softmax 函数）大多受限于内存访问速度，对 HBM 的高频访问不仅增加了内存带宽压力，还显著延长了计算的整体墙钟时间（wall-clock time），从而降低了模型的运行效率。

3. Flash Attention​

FlashAttention 的核心思想可以用两个关键词来概括：分块计算 和 动态重计算。这两种技术的结合，使得注意力机制在保持高效的同时，显著减少了内存占用。

3.1 分块计算：化整为零​

传统的 Softmax 需要一次性加载整个输入数据，才能计算全局的最大值和归一化系数。而 FlashAttention 采用了 增量式计算 的方式，将输入数据分成小块，依次加载到 GPU 的片上缓存（SRAM）中。

我们首先定义一些变量方便后续的讨论：

变量尺寸（shape）说明
Q,K,V\mathbf{Q}, \mathbf{K}, \mathbf{V}N×dN \times d输入矩阵
Qi\mathbf{Q}_iBr×dB_r \times dQ\mathbf{Q} 的第 ii 个行分块
Kj,Vj\mathbf{K}_j, \mathbf{V}_jBc×dB_c \times dK,V\mathbf{K}, \mathbf{V} 的第 jj 个行分块
Sij\mathbf{S}_{ij}Br×BcB_r \times B_c局部注意力分数矩阵
m~ij\tilde{m}_{ij}BrB_r局部行最大值向量
P~ij\tilde{\mathbf{P}}_{ij}Br×BcB_r \times B_c局部未归一化的注意力权重
ℓ~ij\tilde{\ell}_{ij}BrB_r局部行和向量
minewm_i^{\mathrm{new}}BrB_r更新后的全局行最大值
ℓinew\ell_i^{\mathrm{new}}BrB_r更新后的全局行和
Oi\mathbf{O}_iBr×dB_r \times d输出的第 ii 个分块

首先，FlashAttention 将输入矩阵 Q,K,V\mathbf{Q}, \mathbf{K}, \mathbf{V} 划分为若干小块。假设片上缓存的大小为 MM，则 Q\mathbf{Q} 被划分为 Tr=⌈N/Br⌉T_r = \lceil N/B_r \rceil 个块，每块大小为 Br×dB_r \times d；K\mathbf{K} 和 V\mathbf{V} 被划分为 Tc=⌈N/Bc⌉T_c = \lceil N/B_c \rceil 个块，每块大小为 Bc×dB_c \times d。这里 BrB_r 和 BcB_c 的选择基于缓存的大小和特征维度 dd。

对于每一块 Kj\mathbf{K}_j 和 Vj\mathbf{V}_j，FlashAttention 将其从 HBM 加载到 SRAM，然后与每一块 Qi\mathbf{Q}_i 计算局部注意力分数 Sij=QiKjT\mathbf{S}_{ij} = \mathbf{Q}_i \mathbf{K}_j^T。Sij\mathbf{S}_{ij} 的大小为 Br×BcB_r \times B_c，远小于全局矩阵 N×NN \times N。

为了在分块计算中保持数值稳定性，FlashAttention 维护两个全局统计量：行最大值 mi∈RBrm_i \in \mathbb{R}^{B_r} 和行和 ℓi∈RBr\ell_i \in \mathbb{R}^{B_r}。对于每一块 Sij\mathbf{S}_{ij}，计算局部最大值 m~ij\tilde{m}_{ij} 和局部归一化系数 ℓ~ij\tilde{\ell}_{ij}，并根据这些值动态更新全局统计量。

在更新输出矩阵 Oi\mathbf{O}_i 时，FlashAttention 采用增量式的方法，将每一块的计算结果逐步累加。具体公式为：

Oi←diag(ℓinew)−1(diag(ℓi)emi−minewOi+em~ij−minewP~ijVj)\mathbf{O}_i \leftarrow \text{diag}(\ell_i^{\text{new}})^{-1} \left( \text{diag}(\ell_i) e^{m_i - m_i^{\text{new}}} \mathbf{O}_i + e^{\tilde{m}_{ij} - m_i^{\text{new}}} \tilde{\mathbf{P}}_{ij} \mathbf{V}_j \right)

这一公式确保了输出结果与全局计算等价。在每一块计算完成后，更新后的 Oi\mathbf{O}_i、ℓi\ell_i 和 mim_i 被写回 HBM，供后续计算使用。

note

本文不探讨公式的具体推导过程，感兴趣的读者可以参考 [2]

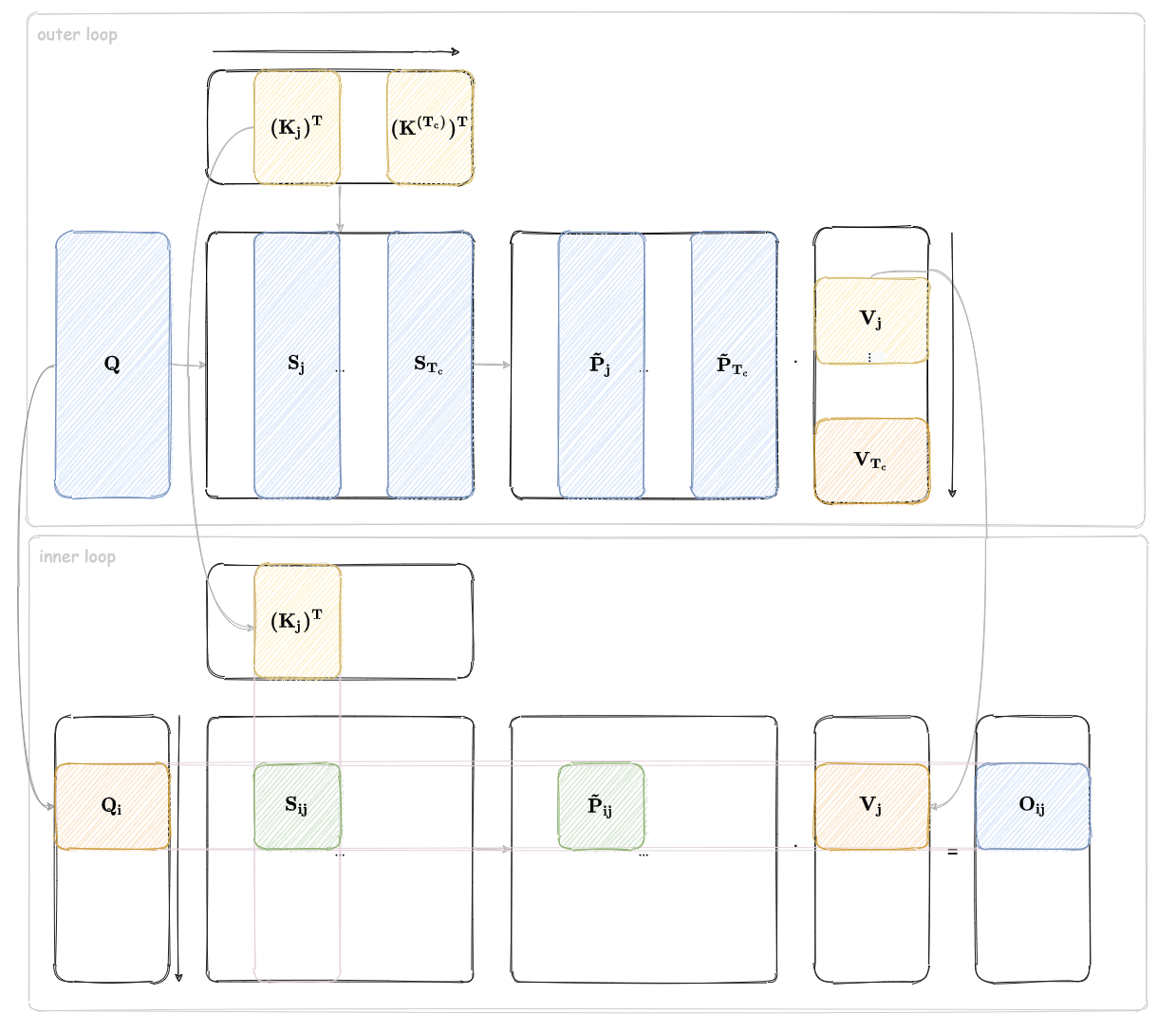
picture 6

上图是 FlashAttention 的分块计算的示意图，外层循环中会对 K\mathbf{K} 和 V\mathbf{V} 进行分块，而内层循环中会对 Q\mathbf{Q} 进行分块。每个外层循环中都会计算得到 Oi,j\mathbf{O_{i,j}}，并将其根据公式更新到 O\mathbf{O} 中。

这里我们以一个最简单的例子来说明更新的过程。

我们以 序列长度 N=4N = 4 、特征维度 d=2d = 2 为例，将输入矩阵 Q,K,V\mathbf{Q}, \mathbf{K}, \mathbf{V} 均分为 2 块，展示 FlashAttention 的分块计算和流式更新过程。假设：

  • Q∈R4×2\mathbf{Q} \in \mathbb{R}^{4 \times 2}，分为 2 块：Q1∈R2×2\mathbf{Q}_1 \in \mathbb{R}^{2 \times 2}, Q2∈R2×2\mathbf{Q}_2 \in \mathbb{R}^{2 \times 2}（每块行数 Br=2B_r = 2 ）。
  • K,V∈R4×2\mathbf{K}, \mathbf{V} \in \mathbb{R}^{4 \times 2}，分为 2 块：K1,V1∈R2×2\mathbf{K}_1, \mathbf{V}_1 \in \mathbb{R}^{2 \times 2}, K2,V2∈R2×2\mathbf{K}_2, \mathbf{V}_2 \in \mathbb{R}^{2 \times 2}（每块行数 Bc=2B_c = 2 ）。

初始状态下：

  • 输出矩阵 O=[00000000]\mathbf{O} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{bmatrix}。
  • 全局统计量：ℓ=[0,0,0,0]T\ell = [0, 0, 0, 0]^T, m=[−∞,−∞,−∞,−∞]Tm = [-\infty, -\infty, -\infty, -\infty]^T。

步骤 1：外层循环 j=1j=1，处理块 K1\mathbf{K}_1， V1\mathbf{V}_1 :

  1. 加载 K1\mathbf{K}_1, V1\mathbf{V}_1 到 SRAM：

    K1=[k11k12k21k22],V1=[v11v12v21v22]\mathbf{K}_1 = \begin{bmatrix} k_{11} & k_{12} \\ k_{21} & k_{22} \end{bmatrix}, \quad \mathbf{V}_1 = \begin{bmatrix} v_{11} & v_{12} \\ v_{21} & v_{22} \end{bmatrix}

  2. 内层循环 i=1i=1，处理块 Q1\mathbf{Q}_1 ：

    • 加载数据：
      Q1=[q11q12q21q22],O1=[0000],ℓ1=[0,0]T,m1=[−∞,−∞]T\mathbf{Q}_1 = \begin{bmatrix} q_{11} & q_{12} \\ q_{21} & q_{22} \end{bmatrix}, \quad \mathbf{O}_1 = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}, \quad \ell_1 = [0, 0]^T, \quad m_1 = [-\infty, -\infty]^T
    • 计算局部注意力分数：
      S11=Q1K1T=[q11k11+q12k12q11k21+q12k22q21k11+q22k12q21k21+q22k22]∈R2×2\mathbf{S}_{11} = \mathbf{Q}_1 \mathbf{K}_1^T = \begin{bmatrix} q_{11}k_{11} + q_{12}k_{12} & q_{11}k_{21} + q_{12}k_{22} \\ q_{21}k_{11} + q_{22}k_{12} & q_{21}k_{21} + q_{22}k_{22} \end{bmatrix} \in \mathbb{R}^{2 \times 2}
    • 局部统计量：
      • 逐行最大值 m~11=[max⁡(S11[1,:]),max⁡(S11[2,:])]T\tilde{m}_{11} = [\max(\mathbf{S}_{11}[1,:]), \max(\mathbf{S}_{11}[2,:])]^T。
      • 未归一化注意力权重 P~11=exp⁡(S11−m~11)\tilde{\mathbf{P}}_{11} = \exp(\mathbf{S}_{11} - \tilde{m}_{11})。
      • 逐行和 ℓ~11=[sum(P~11[1,:]),sum(P~11[2,:])]T\tilde{\ell}_{11} = [\text{sum}(\tilde{\mathbf{P}}_{11}[1,:]), \text{sum}(\tilde{\mathbf{P}}_{11}[2,:])]^T。
    • 更新全局统计量：
      • 全局最大值 m1new=max⁡(m1,m~11)m_1^{\text{new}} = \max(m_1, \tilde{m}_{11})。
      • 全局行和 ℓ1new=em1−m1newℓ1+em~11−m1newℓ~11\ell_1^{\text{new}} = e^{m_1 - m_1^{\text{new}}} \ell_1 + e^{\tilde{m}_{11} - m_1^{\text{new}}} \tilde{\ell}_{11}。
    • 更新输出：
      O1←diag(ℓ1new)−1(diag(ℓ1)em1−m1newO1+em~11−m1newP~11V1)\mathbf{O}_1 \leftarrow \text{diag}(\ell_1^{\text{new}})^{-1} \left( \text{diag}(\ell_1) e^{m_1 - m_1^{\text{new}}} \mathbf{O}_1 + e^{\tilde{m}_{11} - m_1^{\text{new}}} \tilde{\mathbf{P}}_{11} \mathbf{V}_1 \right)
    • 写回 HBM：更新后的 O1\mathbf{O}_1 对应前两行，ℓ1\ell_1 和 m1m_1 同步更新。

  3. 内层循环 i=2i=2，处理块 Q2\mathbf{Q}_2 ：

    • 类似地，加载 Q2=[q31q32q41q42]\mathbf{Q}_2 = \begin{bmatrix} q_{31} & q_{32} \\ q_{41} & q_{42} \end{bmatrix}，计算 S21=Q2K1T\mathbf{S}_{21} = \mathbf{Q}_2 \mathbf{K}_1^T，更新后两行 O2\mathbf{O}_2。

步骤 2：外层循环 j=2j=2，处理块 K2\mathbf{K}_2， V2\mathbf{V}_2 ：

  1. 加载 K2\mathbf{K}_2, V2\mathbf{V}_2 到 SRAM：

    K2=[k31k32k41k42],V2=[v31v32v41v42]\mathbf{K}_2 = \begin{bmatrix} k_{31} & k_{32} \\ k_{41} & k_{42} \end{bmatrix}, \quad \mathbf{V}_2 = \begin{bmatrix} v_{31} & v_{32} \\ v_{41} & v_{42} \end{bmatrix}

  2. 内层循环 i=1i=1，处理块 Q1\mathbf{Q}_1：

    • 加载数据：当前 O1\mathbf{O}_1 已包含来自 V1\mathbf{V}_1 的贡献。
    • 计算局部注意力分数：
      S12=Q1K2T=[q11k31+q12k32q11k41+q12k42q21k31+q22k32q21k41+q22k42]∈R2×2\mathbf{S}_{12} = \mathbf{Q}_1 \mathbf{K}_2^T = \begin{bmatrix} q_{11}k_{31} + q_{12}k_{32} & q_{11}k_{41} + q_{12}k_{42} \\ q_{21}k_{31} + q_{22}k_{32} & q_{21}k_{41} + q_{22}k_{42} \end{bmatrix} \in \mathbb{R}^{2 \times 2}
    • 更新统计量：根据 S12\mathbf{S}_{12} 的局部最大值和行和，更新 m1newm_1^{\text{new}} 和 ℓ1new\ell_1^{\text{new}}。
    • 更新输出：
      O1←diag(ℓ1new)−1(diag(ℓ1)em1−m1newO1+em~11−m1newP~12V2)\mathbf{O}_1 \leftarrow \text{diag}(\ell_1^{\text{new}})^{-1} \left( \text{diag}(\ell_1) e^{m_1 - m_1^{\text{new}}} \mathbf{O}_1 + e^{\tilde{m}_{11} - m_1^{\text{new}}} \tilde{\mathbf{P}}_{12} \mathbf{V}_2 \right)
    • 结果等价于全局 Softmax：最终 O1\mathbf{O}_1 为前两行注意力结果的加权和。

  3. 内层循环 i=2i=2，处理块 Q2\mathbf{Q}_2：

    • 类似地，计算 S22=Q2K2T\mathbf{S}_{22} = \mathbf{Q}_2 \mathbf{K}_2^T，更新后两行 O2\mathbf{O}_2。

通过这种分阶段、分块处理的方式，FlashAttention 在不牺牲计算精度的前提下，显著提升了注意力机制的效率，成为处理长序列任务的利器。

3.2 动态重计算：用时间换空间​

在反向传播阶段，传统的注意力机制需要存储前向传播生成的完整注意力矩阵，这进一步加剧了内存压力。FlashAttention 采用了 动态重计算 的策略：在前向传播中，只存储必要的中间结果（如最大值和归一化系数），而在反向传播时，按需重新计算注意力矩阵。

我们的文章里面展示只实现前向传播的计算，反向传播的详细过程可以参考 [2]。

参考文献​

[1] Andrei Ivanov, Nikoli Dryden, Tal Ben-Nun, Shigang Li, and Torsten Hoefler. Data movement is all you need: A case study on optimizing transformers. Proceedings of Machine Learning and Systems, 3:711–732, 2021 [2] https://zhuanlan.zhihu.com/p/669926191 [3] http://www.zh0ngtian.tech/posts/49b73eba.html