im2col + gemm 实现卷积
本文让我们使用 im2col 和 gemm 来实现卷积操作。
1. im2col 算子实现
首先让我们来实现 im2col 算子,这个算子的作用是将输入的图像转换为矩阵,这样我们就可以使用矩阵乘法来实现卷积操作。这个算子本身并没有太多需要能够优化的地方,我们需要做的就是按照上一篇文章中给出的 im2col 的定义来实现这个算子。
先让我们简单回顾一下 im2col 操作,假设我们有一个大小为 [, , , ] 的输入张量,其中 是批大小, 是通道数, 和 是图像的高度和宽度,我们需要将这个输入张量转换为一个大小为 [, , , , , ] 的输出张量,其中 是通道数, 是卷积核的大小, 和 是输出图像的高度和宽度。下图是 im2col 的示意图:
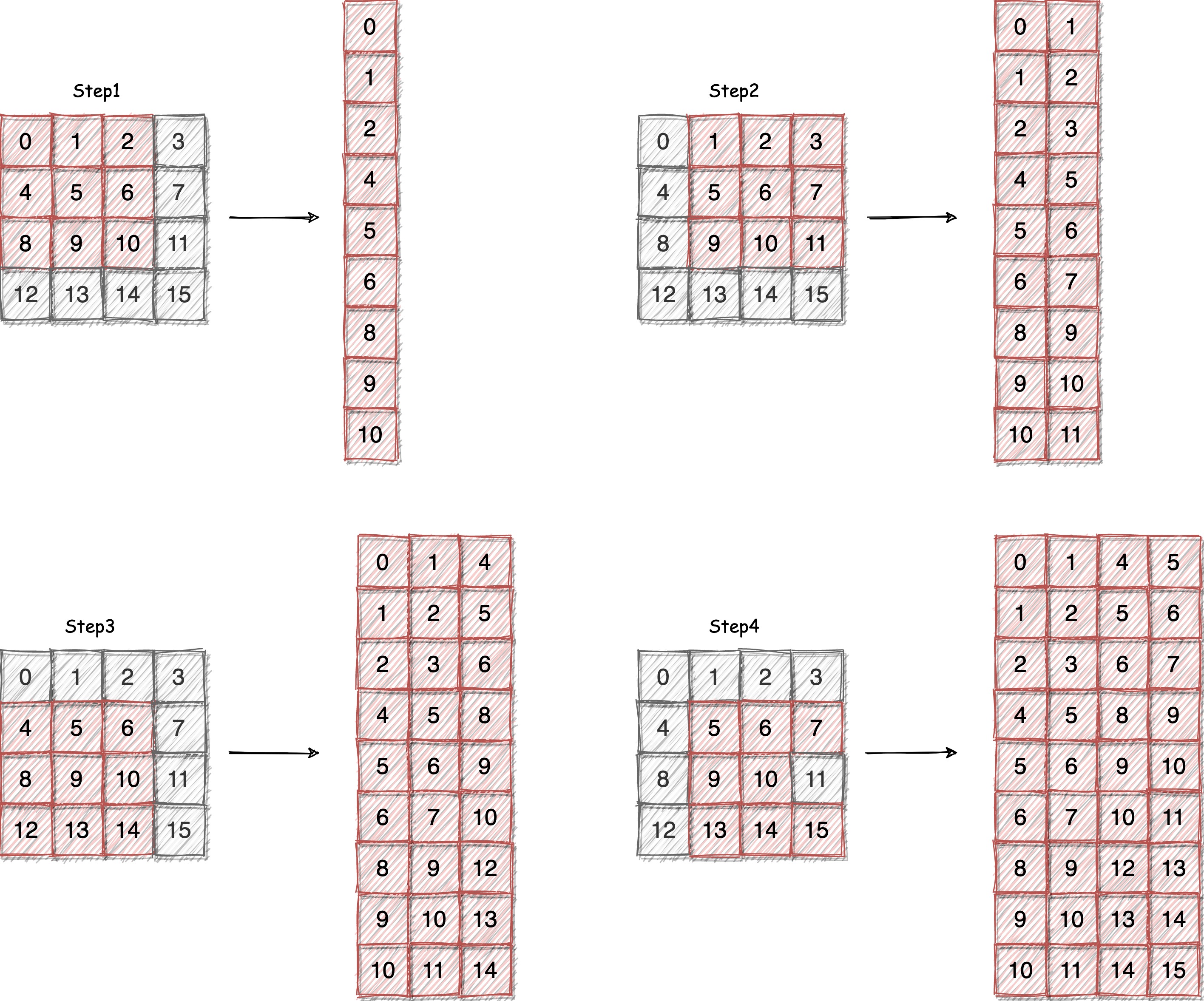
简单来说就是将输入图像中每个卷积核对应的位置的像素值放到一个矩阵中。输入图像一个通道的大小是 H * W, im2col 对应的输出矩阵的大小是 KH * KW * H' * W'。我们这个 Kernel 的思路就是让每个线程负责一次将卷积核对应的像素值放到输出矩阵中,也就是输出一条矩阵的这个过程。在了解了这个过程之后,我们就可以开始实现这个算子了。
首先我们先来定义这个算子的接口,该算子的输入是一个大小为 [, , , ] 的输入张量,输出是一个大小为 [, , , , , ] 的输出张量。我们可以使用下面的代码来定义这个算子的接口:
注意,这里为什么输出的 shape 不是 [, , , , , ] 而是 [, , , , , ] ?我们可以保留这个疑问,后面我们会解释这个问题。
template <typename T>
__global__ void im2col_kernel(const int n,
T *data_x,
T *data_y,
const int batches, // 批大小
const int inner_size_x, // 每个样本(或批次)中单个通道的输入数据的大小
const int inner_size_y, // 每个样本(或批次)中单个通道的输出数据的大小
const int x_height, // 输入图像的高度
const int x_width, // 输入图像的宽度
const int kernel_height, // 卷积核的高度
const int kernel_width, // 卷积核的宽度
const int pad_height, // 填充的高度
const int pad_width, // 填充的宽度
const int stride_height, // 步长的高度
const int stride_width, // 步长的宽度
const int dilation_height, // 膨胀的高度
const int dilation_width, // 膨胀的宽度
const int y_height, // 输出图像的高度
const int y_width, // 输出图像的宽度
const int inner_size_c // 每个批次中通道数乘以输出张量的大小
);
接下来我们来实现这个算子的代码,首先为了方便后面的计算,我们先定义一些变量:
int batch = index / inner_size_c, idx = index % inner_size_c;
int w_out = idx % y_width, id = idx / y_width;
int h_out = id % y_height, channel_in = id / y_height;
int channel_out = channel_in * kernel_height * kernel_width;
接下来计算输入图像中对应输出位置的起始位置,并设置输入和输出数据指针。
for (int i = 0; i < kernel_height; ++i)
{
for (int j = 0; j < kernel_width; ++j)
{
int h = h_in + i * dilation_height; // 计算输入图像的高度
int w = w_in + j * dilation_width; // 计算输入图像的宽度
// 计算输入图像的索引, 如果索引超出了输入图像的大小,则设置为 0
*out = (h >= 0 && w >= 0 && h < x_height && w < x_width)
? in[i * dilation_height * x_width + j * dilation_width]
: static_cast<T>(0);
// 更新输入和输出数据指针
out += y_height * y_width * batches;
}
}
为了更加方便的使用 im2col_kernel 函数,我们还需要定义一个包装函数:
template <typename T>
void cuda_im2col(const int batches, // 批大小
const int x_channel, // 输入图像的通道数
const int x_height, // 输入图像的高度
const int x_width, // 输入图像的宽度
const int y_out_plane, // 输出图像的通道数
const int y_height, // 输出图像的高度
const int y_width, // 输出图像的宽度
const int kernel_height, // 卷积核的高度
const int kernel_width, // 卷积核的宽度
const int stride_height, // 步长的高度
const int stride_width, // 步长的宽度
const int dilation_height, // 膨胀的高度
const int dilation_width, // 膨胀的宽度
const int pad_height, // 填充的高度
const int pad_width, // 填充的宽度
T *x, // 输入数据
T *y // 输出数据)
{
// 计算输入和输出数据的大小
const int inner_size_y = y_out_plane * y_height * y_width;
const int inner_size_x = x_channel * x_height * x_width;
const int inner_size_c = x_channel * y_height * y_width;
// 计算总的卷积核的数量
const int num_kernels = batches * inner_size_c;
// 设置线程块的大小和数量
const int blockSize = std::max(std::min(MaxBlockSize, num_kernels), static_cast<int>(1));
// 计算线程块的数量
const int gridSize = (num_kernels + blockSize - 1) / blockSize;
// 调用 im2col_kernel 函数
im2col_kernel<T><<<gridSize, blockSize>>>(num_kernels,
x,
y,
batches,
inner_size_x,
inner_size_y,
x_height,
x_width,
kernel_height,
kernel_width,
pad_height,
pad_width,
stride_height,
stride_width,
dilation_height,
dilation_width,
y_height,
y_width,
inner_size_c);
}
2. gemm 算子实现
接下来我们来实现 gemm 算子,这个算子的作用是将两个矩阵相乘,我们这里使用之前文章中介绍的二维 Thread Tile 并行优化 矩阵乘法优化方法来实现这个算子。
在用这个算子之前,我们需要先考虑一个问题:矩阵乘的输入矩阵和结果矩阵的大小是多少? 输入 im2col 的矩阵大小是 [, , , ] ,输出 im2col 的矩阵大小是 [, , , , , ],卷积核的大小是 [, , , ]。
这里也就解释了为什么我们的 im2col 的输出矩阵的大小是 [, , , , , ] 而不是 [, , , , , ],因为我们的卷积核是 [, , , ],如果我们的输出矩阵的大小是 [, , , , , ],那么我们在计算卷积的时候就需要将卷积核转置,这样会增加计算的复杂度,所以我们选择了 [, , , , , ] 这种方式。
我们可以发现卷积核和 im2col 输出的矩阵相乘后的大小是 [, , , ],这个大小和我们平时使用的卷积操作的输出大小不太一样,所以我们需要对这个结果进行转置,转置后的大小就是 [, , , ],这个大小和我们平时使用的卷积操作的输出大小是一样的。
已经忘了矩阵乘法的实现方法的同学可以参考之前的文章 二维 Thread Tile 并行优化,它的主要优化思路是将输入矩阵和输出矩阵分块,然后使用线程块中的线程来计算这些块的结果,这样可以减少全局内存的访问次数,提高计算效率。
但是这个 Kernel 并不能直接用到我们的卷积操作中,我们需要做如下的修改:
- 添加判断条件,防止越界访问;
- 将输出矩阵在保存的时候进行转置。
下面我们一起来实现这个代码,首先我们需要定义一些常量方便后续使用:
// 我们在这个线程块中要计算的输出块
const uint c_row = blockIdx.y;
const uint c_col = blockIdx.x;
// 一个线程块中的线程负责计算 TM*TN 个元素
const uint num_threads_block_tile = (BM * BN) / (TM * TN);
// 计算线程的位置
const uint thread_row = threadIdx.x / (BN / TN);
const uint thread_col = threadIdx.x % (BN / TN);
// 用于避免越界访问
int global_c_index = c_row * BM * N + c_col * BN; // 计算C矩阵的全局索引位置
int global_m_pos = c_row * BM * K; // A矩阵全局位置
int global_n_pos = c_col * BN; // B矩阵全局位置
const uint m_size = M * K; // A矩阵的大小
const uint n_size = N * K; // B矩阵的大小
assert((BM * BN) / (TM * TN) == blockDim.x);
// 计算输出矩阵的位置
const uint A_inner_row = threadIdx.x / BK; // A矩阵内部行索引
const uint A_inner_col = threadIdx.x % BK; // A矩阵内部列索引
const uint stride_a = num_threads_block_tile / BK; // A矩阵的跨步
const uint B_inner_row = threadIdx.x / BN; // B矩阵内部行索引
const uint B_inner_col = threadIdx.x % BN; // B矩阵内部列索引
const uint stride_b = num_threads_block_tile / BN; // B矩阵的跨步
这些代码除了添加了用于避免越界访问的代码外,其他的代码和之前的实现是一样的。这里不再多做解释。
接下来我们需要定义一些共享内存,线程块的结果和寄存器变量:
// 申请共享内存
__shared__ float A_shared[BM * BK];
__shared__ float B_shared[BK * BN];
// 用于保存线程块的结果
float thread_results[TM * TN] = {0.0};
float reg_m[TM] = {0.0};
float reg_n[TN] = {0.0};
// 外层循环
for (uint bkIdx = 0; bkIdx < K; bkIdx += BK)
{
... // 每个线程的具体逻辑
}
然后我们需要在内核的外层循环中,将矩阵 A 和矩阵 B 的数据加载到共享内存中:
// 加载数据到共享内存
for (uint load_offset = 0; load_offset < BM; load_offset += stride_a)
{
A_shared[(A_inner_row + load_offset) * BK + A_inner_col] =
(global_m_pos + (A_inner_row + load_offset) * K + A_inner_col < m_size) ? A[(A_inner_row + load_offset) * K + A_inner_col] : 0.0f;
}
for (uint load_offset = 0; load_offset < BK; load_offset += stride_b)
{
B_shared[(B_inner_row + load_offset) * BN + B_inner_col] =
(global_n_pos + (B_inner_row + load_offset) * N + B_inner_col < n_size) ? B[(B_inner_row + load_offset) * N + B_inner_col] : 0.0f;
}
__syncthreads();
// 移动数据指针
A += BK;
B += BK * N;
global_m_pos += BK;
global_n_pos += BK * N;
请注意,这里我们在加载数据的时候,我们需要判断是否越界,如果越界则设置为 0。因为卷积运算经常会遇到越界的情况,所以我们需要在这里进行处理。以前我们主要是学习矩阵乘法,测试的例子都是 512 512 或者 1024 1024 这种大小的矩阵,这种情况下越界的情况比较少,所以我们没有处理这种情况。
下一步我们需要计算矩阵乘法的结果, 我们需要计算 BM * BN 个结果, 并将这一步的结果累加到 thread_results 中。
// 计算矩阵乘法的结果
for (uint dot_idx = 0; dot_idx < BK; dot_idx++)
{
// 将数据加载到寄存器中
for (uint i = 0; i < TM; i++)
{
reg_m[i] = A_shared[(thread_row * TM + i) * BK + dot_idx];
}
for (uint i = 0; i < TN; i++)
{
reg_n[i] = B_shared[dot_idx * BN + thread_col * TN + i];
}
// 计算矩阵乘法的结果
for (uint res_idx_m = 0; res_idx_m < TM; res_idx_m++)
{
for (uint res_idx_n = 0; res_idx_n < TN; res_idx_n++)
{
thread_results[res_idx_m * TN + res_idx_n] += reg_m[res_idx_m] * reg_n[res_idx_n];
}
}
}
// 移动数据指针
__syncthreads();
最后我们需要将 thread_results 中的结果保存到全局内存中,在保存的时候我们需要将结果转置,这里的转置坐标计算看起来难以理解,建议读者画图来理解这个过程(因为我当时就是对着图写出来的,过几天让我自己去看我不对着图也看不懂(x))。
int inner_y_size = y_height * y_width; // 计算Y矩阵的内部尺寸
int res_inner_index, g_index, batch_id, channel_id, inner_offset;
int conv_idx;
if (global_c_index >= M * N) // 如果全局索引超出范围,直接返回
{
return;
}
for (uint res_idx_m = 0; res_idx_m < TM; res_idx_m++)
{
for (uint res_idx_n = 0; res_idx_n < TN; res_idx_n++)
{
if (c_row * BM + thread_row * TM + res_idx_m < M && c_col * BN + thread_col * TN + res_idx_n < N)
{
// 计算结果在C矩阵中的内部索引
res_inner_index = (thread_row * TM + res_idx_m) * N + thread_col * TN + res_idx_n;
// 计算全局索引
g_index = global_c_index + res_inner_index;
// 计算内部偏移
inner_offset = g_index % inner_y_size;
// 计算 batch ID
batch_id = (g_index % (inner_y_size * batch)) / inner_y_size;
// 计算 channel ID
channel_id = g_index / (inner_y_size * batch);
// 根据batch ID、channel ID和内部偏移计算卷积索引
conv_idx = batch_id * (kernel_num * y_height * y_width) + channel_id * (y_height * y_width) + inner_offset;
// 将计算结果写入C矩阵
C[conv_idx] = thread_results[res_idx_m * TN + res_idx_n];
}
}
}
同样为了方便使用,我们还需要定义一个包装函数:
void cuda_gemm(float *A,
float *B,
float *C,
int M,
int N,
int K,
int batch,
int kernel_num,
int y_height,
int y_width)
{
const uint BK = 8;
const uint TM = 8;
const uint TN = 8;
if (M >= 128 && N >= 128)
{
const uint BM = 128;
const uint BN = 128;
dim3 grid_size(CEIL_DIV(N, BN), CEIL_DIV(M, BM));
dim3 block_size((BM * BN) / (TM * TN));
sgemm_blocktiling_2d_kernel<BM, BN, BK, TM, TN>
<<<grid_size, block_size>>>(A, B, C, M, N, K, batch, kernel_num, y_height, y_width);
}
else
{
const uint BM = 64;
const uint BN = 64;
dim3 grid_size(CEIL_DIV(N, BN), CEIL_DIV(M, BM));
dim3 block_size((BM * BN) / (TM * TN));
sgemm_blocktiling_2d_kernel<BM, BN, BK, TM, TN>
<<<grid_size, block_size>>>(A, B, C, M, N, K, batch, kernel_num, y_height, y_width);
}
}
这样我们就实现了 gemm 算子的代码,接下来我们就可以使用这两个算子来实现卷积操作了。
3. 卷积操作实现
首先我们需要调用 im2col 算子将输入图像转换为矩阵,然后调用 gemm 算子将转换后的矩阵和卷积核进行矩阵乘法,最后将结果保存到输出张量中。
cuda_im2col(batch_size,
x_channel,
x_height,
x_width,
y_out_plane,
y_height,
y_width,
kernel_height,
kernel_width,
stride_height,
stride_width,
dilation_height,
dilation_width,
pad_height,
pad_width,
pIn_device,
pInCol_device);
KernelErrChk();
cudaDeviceSynchronize();
cuda_gemm(pWeight_device,
pInCol_device,
pOut_device,
kernel_numbers,
batch_size * y_height * y_width,
x_channel * kernel_height * kernel_width,
batch_size,
kernel_numbers,
y_height, y_width);
4. 编译和运行
这个代码我们提供了 Makefile 文件,可以直接使用 make 命令来编译代码,编译完成后运行 bash job.sh 可以自动输入样例数据并运行代码。
5. 总结
本文我们实现了 im2col 和 gemm 算子,然后使用这两个算子来实现卷积操作。下一篇文章我们会介绍如何把 im2col 给优化掉,让我们的卷积操作更加高效。
References
- https://siboehm.com/articles/22/CUDA-MMM
- https://space.keter.top/docs/high_performance/GEMM%E4%BC%98%E5%8C%96%E4%B8%93%E9%A2%98/%E5%85%B1%E4%BA%AB%E5%86%85%E5%AD%98%E7%BC%93%E5%AD%98%E5%9D%97
- https://space.keter.top/docs/high_performance/GEMM%E4%BC%98%E5%8C%96%E4%B8%93%E9%A2%98/%E4%B8%80%E7%BB%B4Thread%20Tile%E5%B9%B6%E8%A1%8C%E4%BC%98%E5%8C%96
- https://github.com/AndSonder/UNIVERSAL_SGEMM_CUDA